Курсы подготовки к ЕГЭ по математике в Лобне
Улучшение оценок в школе уже после трех занятий!
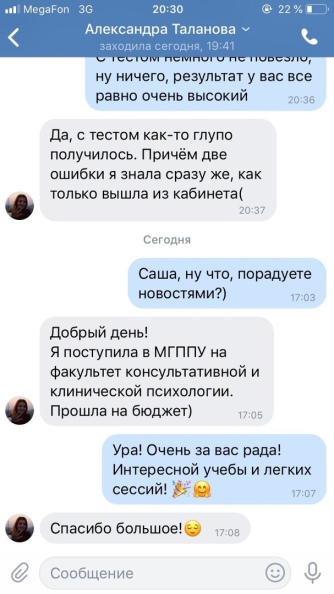
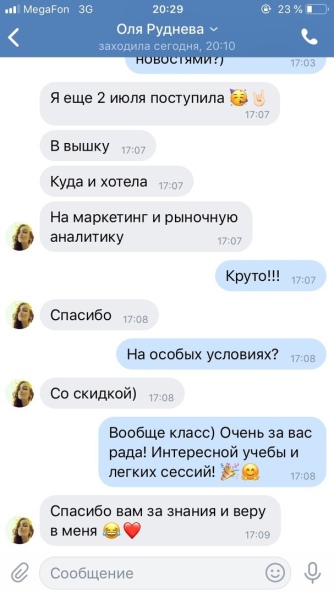
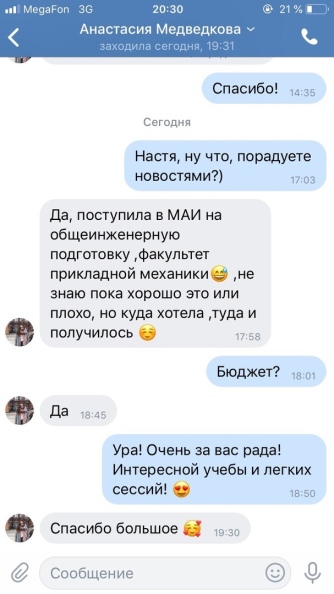
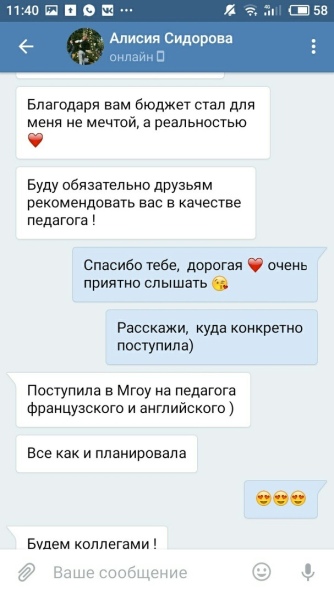
Наш рейтинг за 9 лет работы



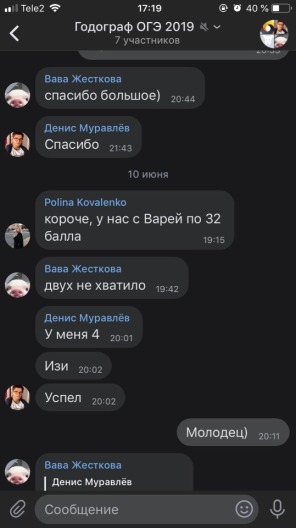
Обучающий курс включает в себя не только теорию, но и практику. Группа сначала изучает первую часть – задачи с кратким ответом, что считается базовым уровнем, а потом переходит к второй части. Задания с кратким ответом принесут ученикам до 11 первичных баллов (64 вторичных).
Также курс включает в себя материалы по правильному оформлению задач из второй части ЕГЭ. Мы расскажем про все нюансы оформления задач из второй части ЕГЭ
- Алгебра и начала анализа (8 заданий)
- Геометрия (4 задания)
- Реальная математика (6 заданий)
Обычная подготовка = 55 баллов
Средний балл по ЕГЭ в России за 2025 год — 55 баллов
- Тренируют навык нарешеванием тестов
- Считают, что зазубрить материал достаточно
Комплексная подготовка в Годографе на 80+ баллов по математике
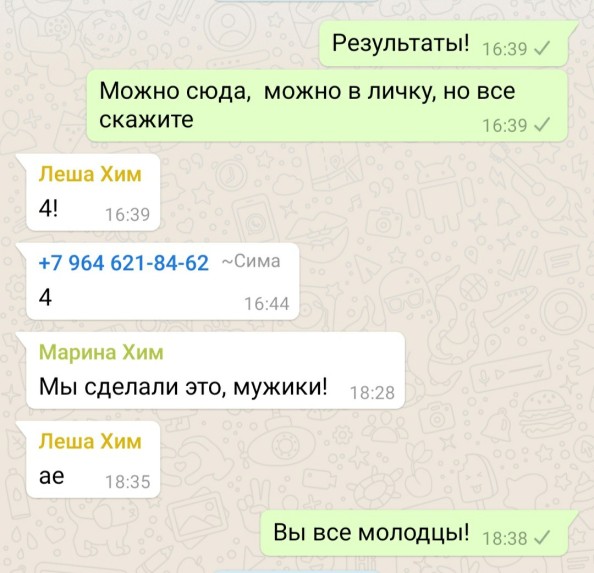
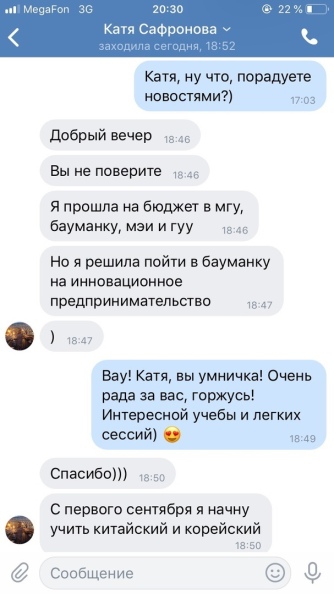
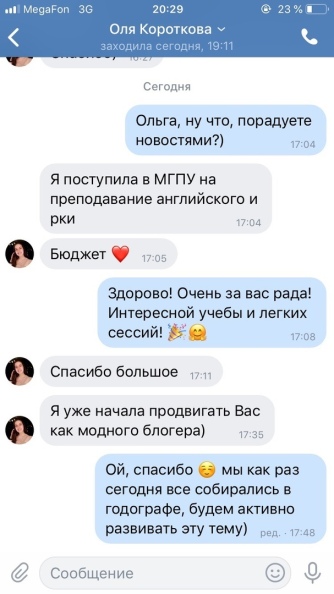
Средний балл учеников Годографа в 2025 году — 80 баллов.
- Создаем фундамент знаний предмета
- Контролируем процесс обучения
- Контролируем успеваемость
- Поддерживаем дисциплину
- Улучшаем психологическое состояние
- Создаем внутреннюю мотивацию к учебе
Только комплексная подготовка поможет сдать ЕГЭ по математике на 80+
Комплексный подход Годографа
Глубокое понимание предмета
Только при полном понимании предмета ученик сможет решать 2 часть ЕГЭ и его не собьет с толку изменение формулировок заданий.
Дисциплина
У ученика выработается привычка много работать над экзаменом. У него будет четкое расписание занятий и дедлайны выполнения домашней работы.
Контроль процесса обучения
Если наставник видит, что ученик не успевает по программе или у него маленький ежемесячный прирост баллов, то индивидуальный процесс обучения вовремя корректируется.
Внутренняя мотивация
С помощью педагога-наставника и атмосферы ученику будет в удовольствие сам процесс обучения. Он будет разбираться в процессе и гореть желанием сдать экзамен как можно лучше.
Психологическая поддержка
Чтобы не потерять баллы из-за нервов на экзамене, ученику надо научиться нейтрализовать стресс и справляться с волнением. В нашей команде с помощью психологов это сделать намного проще.
Контроль успеваемости
Ученик должен усвоить каждую тему на 100%, поэтому мы контролируем усвоение тем и заданий ЕГЭ, и корректируем темп прохождения материала.



Помогите вашему ребенку сдать ЕГЭ по математике на высокий балл
Запишите ребенка на бесплатную диагностику знаний с педагогом уже сейчас!
Контроль процесса обучения – залог 80+ баллов на ЕГЭ по математике
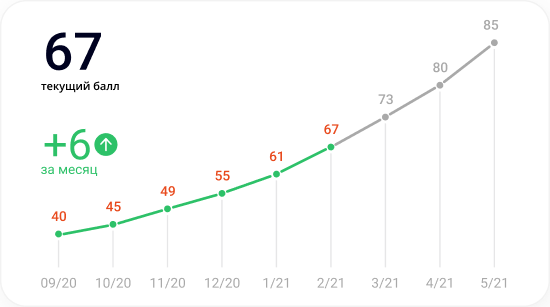
Каждый месяц пробный ЕГЭ
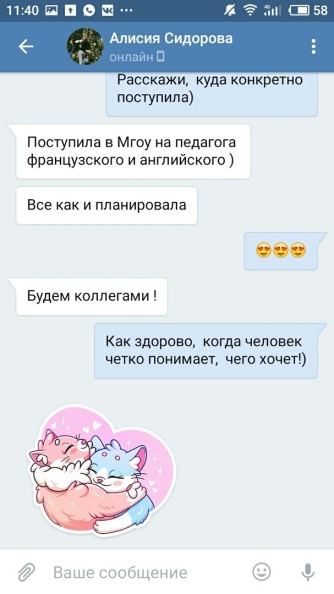
Родители и ученик видят динамику роста благодаря ежемесячным тестам ЕГЭ. Мы вовремя выявляем пробелы в предмете, чтобы корректировать обучение.
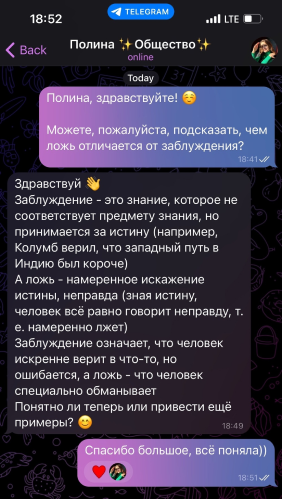
Педагог на связи с учениками 24/7
Педагог в чате в соцсети всегда поможет ученику разобраться в материале и ответит на вопросы по домашнему заданию.

СМС-отчетность родителям после урока
После каждого урока родитель получает СМС с оценками ребенка за работу на уроке, тестирование и домашнее задание.

Ученик занимается в небольшой группе, изначально разделенной по уровню знаний, но во время обучения он может перевестись в более сильную группу.


учебный год 2025-2026
|
Дата заключения договора |
Стоимость 4 занятий | Стоимость 36 занятий
(- 10%) |
Сравнительная стоимость
условного месяца обучения при оплате за 4 занятия / за 36 занятий |
| с 07.01.2026 | 9 500 ₽ | 76 950 ₽ | 9 500 / 8 550 ₽ |
Многодетным семьям предоставляется скидка 5%
СТОИМОСТЬ 7-МИ ДНЕВНОГО ТРЕНИНГА ПО ПРОФОРИЕНТАЦИИ: 15 000 ₽
В стоимость включены: 3 очных занятия по 3 часа, работа с куратором в течение недели онлайн, все материалы и кофе-брейки,
обратная связь родителям и ребенку по итогам программы.
Подробности на странице "Профориентация"




Обратный звонок
Оставьте заявку и мы перезвоним вам в течение ближайшего часа.
г. Лобня, ул. Чехова, 31, 2 этаж
+7 (985) 178-45-05
Email: lobnya@godege.ruРежим работы: с 10:00 до 18:00